Моделирование времени обработки деталей из листа с использованием дробно-степенных рядов и генетического алгоритма
В расчетах коэффициентов загрузки оборудования и его количества, выполняемых при проектировании производства, необходимо использовать время обработки программы деталей для всей номенклатуры. Как правило, определение норм времени выполняется методом хронометража обработки подобных деталей или моделированием обработки каждой детали в CAM-системах.
Это трудоемкий процесс, значительно увеличивающий длительность проектирования. Часто используют результаты расчета норм времени по деталям-представителям. При этом из всей номенклатуры деталей формируются группы, объединяющим признаком которых является подобие операционного технологического процесса. Для одной или нескольких деталей-представителей из группы рассчитывается время обработки. Затем, общее время обработки группы деталей определяется произведением их программы производства на среднее время обработки деталей-представителей. При использовании этого метода длительность проектирования снижается, но погрешность нормирования часто оказывается недопустимой для практического использования.
Сократить сроки проектирования и обеспечить требуемую точность нормирования позволит моделирование времени обработки деталей-представителей, результаты которого используются для расчета времени обработки всей группы деталей.
Представим поставленную задачу моделирования времени обработки как задачу математического программирования. Для таких задач характерно большое количество параметров (многопараметрическая задача), изменяя которые в заданных пределах определяют значения критериев оптимальности (многокритериальная задача).
Рассматривая критерии оптимальности, образующие целевую функцию, можно найти их оптимальные значения. Проблема состоит в том, чтобы выбрать наилучшее решение в условиях, когда гиперповерхность, задаваемая целевой функцией образована несколькими локальными экстремумами (мультимодальность). При этом один из экстремумов глобальный, соответствует решению задачи и существует вероятность определения одного из локальных экстремумов как глобального. Другая проблема – когда гиперповерхность, задаваемая целевой функцией имеет «разрывы», «грани» или «плато». В результате невозможно применить эффективные вычислительные алгоритмы, основанные на использовании производных.
Среди методов решения многопараметрических, многокритериальных и мультимодальных задач наиболее эффективными являются алгоритмы ЛП-поиска [1, 2], Поведенческие алгоритмы, например метод Пчелиного роя (Bees Algorithm) [3 - 5] и Генетические алгоритмы [6 - 10].
В данной работе приведен комбинированный генетический алгоритм (КГА) и результаты его тестирования. Тестирование выполнялось решением тестовых задач и задач аппроксимации табличных значений времени обработки деталей из листа как функции нескольких переменных дробно-степенными рядами. Проводится сравнение результатов решения с решением, полученным численным методом Ньютона.
Постановка задачи математического программирования
Задаются пределы изменения управляемых параметров ![]() или «параметрические ограничения»
или «параметрические ограничения»![]() ,
, ![]() которые образуют в r-мерном параллелепипеде П допустимое множество
которые образуют в r-мерном параллелепипеде П допустимое множество![]() . Длина граней параллелепипеда
. Длина граней параллелепипеда ![]() определяет «длину интервала неопределенности».
определяет «длину интервала неопределенности».
«Целевая функция» или «критерий оптимальности» ![]() позволяет количественно сравнить альтернативные варианты управляемых параметров.
позволяет количественно сравнить альтернативные варианты управляемых параметров.
«Принцип оптимальности»: оптимальное решение найдено, когда все критерии оптимальности улучшили свои значения, т.е. те, которые должны увеличиться - увеличились, а те которые должны уменьшиться - уменьшились. Этот принцип называется принципом оптимальности по Парето, согласно которому требуется найти такое множество Парето ![]() , для которого
, для которого ![]() , где
, где ![]() - целевая функция. В результате решения определяют вектор управляемых параметров
- целевая функция. В результате решения определяют вектор управляемых параметров ![]() , принадлежащий множеству P и являющейся наиболее предпочтительным (или оптимальным) из всех векторов этого множества.
, принадлежащий множеству P и являющейся наиболее предпочтительным (или оптимальным) из всех векторов этого множества.
Комбинированный генетический алгоритм.
Алгоритм (рис. 1) построен на основе комбинации двух методов: «Пассивного поиска минимума» [11] и «Генетического алгоритма»:
- Формирование вариантов управляемых параметров модели (детерминированный метод). Для каждого управляемого параметра выполняется деление интервала неопределенности
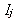 на
на 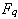 равноотстоящих точек, где
равноотстоящих точек, где 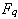 – число из последовательности Фибоначчи. Порядковый номер q ? 10 числа Фибоначчи назначается как целая часть числа, рассчитанного на основе максимальной длины интервала неопределенности
– число из последовательности Фибоначчи. Порядковый номер q ? 10 числа Фибоначчи назначается как целая часть числа, рассчитанного на основе максимальной длины интервала неопределенности 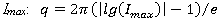 . Формируется матрица управляемых параметров: строки матрицы представляют линейную сетку по каждому управляемому параметру, столбцы матрицы содержат варианты управляемых параметров.
. Формируется матрица управляемых параметров: строки матрицы представляют линейную сетку по каждому управляемому параметру, столбцы матрицы содержат варианты управляемых параметров. - Расчет значений критериев оптимальности для вариантов управляемых параметров. В результате решения уравнений модели для каждого из вариантов управляемых параметров формируется матрица критериев оптимальности.
- Поиск минимального значения целевой функции. Минимальное значение целевой функции
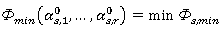 , где
, где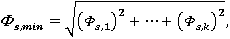 , s – номер итерации поиска;
, s – номер итерации поиска; 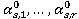 - точка промежуточного оптимума (если s = 0, «нулевая точка»).
- точка промежуточного оптимума (если s = 0, «нулевая точка»). - Сужение интервала неопределенности около точки промежуточного оптимума:
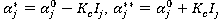 , где
, где 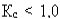 коэффициент сужения интервала неопределенности.
коэффициент сужения интервала неопределенности. - Скрещивание.
- Формирование начальной «популяции особей» (формирование вариантов управляемых параметров) детерминированным методом и методом случайных чисел.
- Скрещивание «особей» методом «панмиксии». Генерируются случайные числа
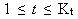 (целые числа) и
(целые числа) и 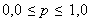 . Ситуация совпадения чисел t ислючается. Каждому «гену» (или управляемому параметру) ставится в соответствие одно из чисел t. Брачная пара образуется выбором двух пар случайных чисел: t1 и t2; p1 и p2 = 1,0 - p1. Формируется новый «ген» (новое значение управляемого параметра)
. Ситуация совпадения чисел t ислючается. Каждому «гену» (или управляемому параметру) ставится в соответствие одно из чисел t. Брачная пара образуется выбором двух пар случайных чисел: t1 и t2; p1 и p2 = 1,0 - p1. Формируется новый «ген» (новое значение управляемого параметра) 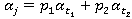 . Новые «гены» образуют новые «хромосомы» (вариант значений управляемых параметров) и новое поколение из Kt «особей» (все варианты значений управляемых параметров).
. Новые «гены» образуют новые «хромосомы» (вариант значений управляемых параметров) и новое поколение из Kt «особей» (все варианты значений управляемых параметров). - Вычисление «пригодностей хромосом». Для каждой «хромосомы» из начальной «популяции» вычисляется ее «пригодность» (или для каждого варианта управляемых параметров вычисляется значение целевой функции). Минимальному значению «пригодности» соответствует «перспективная хромосома». Поиск минимального значения «пригодности» (поиск минимального значения целевой функции) выполняется по методу п.3.
- Мутации. Изменению подвергается каждый «ген» перспективной хромосомы
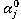 в пределах
в пределах 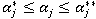 . Вычисляются «пригодности» мутированных хромосом и выполняется поиск минимального значения «пригодностей» по методу п.3.
. Вычисляются «пригодности» мутированных хромосом и выполняется поиск минимального значения «пригодностей» по методу п.3. - Расширение интервала неопределенности около точки промежуточного оптимума:
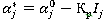 , где
, где 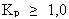 – коэффициент расширения интервала неопределенности.
– коэффициент расширения интервала неопределенности. - Остановка вычислений выполняется контролем принятого предельного числа циклов поиска S (количества «поколений особей») и заданной величины изменения целевой функции ? на каждом шаге итерации.
Пассивный поиск минимума реализован в первых четырех блоках алгоритма. В результате его работы определяется точка промежуточного оптимума и работа генетического алгоритма (блоки 5 и 6) начинается на более узких интервалах неопределенности, которые содержат искомые оптимальные значения управляемых параметров. Циклическое сужение и расширение интервалов неопределенности обеспечивает исследование большого числа вариантов управляемых параметров, позволяющее надежно определить минимальное значение целевой функции.
Тестирование алгоритма.
Использовано два метода тестирования: поиск корней уравнения с двумя неизвестными и метод аппроксимации табличных значений дробно-степенным рядом.
Поиск корней уравнения с двумя неизвестными выполнен для моделей, приведенных в табл. 1. Поверхность, отображающая целевую тестовую функцию этих моделей, содержит несколько локальных минимумов (рис. 2), поэтому надежность работы алгоритма оценивается по точности определения глобального минимума, соответствующего решению уравнения модели.
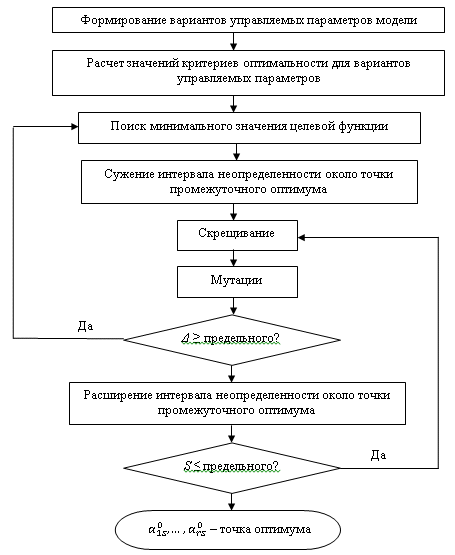
Рис. 1. Блок схема алгоритма

Таблица 1. Мультимодальные модели для тестирования КГА

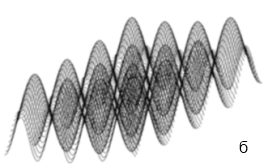
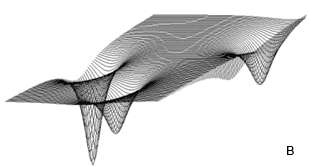
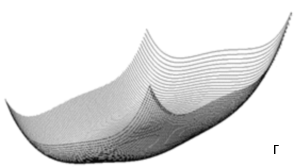
Рис. 2. Фрагменты поверхностей, отображающие тестовые функции в пределах параметрических ограничений (табл. 1): а – Розенброка; б - Растригина; в – Шекеля; г – Химмельблау.
Таблица 3.
Описательная статистика тестовых функций, полученная с использованием КГА (?1 и ?2 – корни уравнений)
| Описательная статистика | Функция | |||||||
| Розенброка | Растригина | Шекеля | Химмельблау | |||||
| ?1 = 1,0 | ?2 = 1,0 | ?1 = 0,0 | ?2 = 0,0 | ?1 = 2,0 | ?2 = 10,0 | ?1 = 3,0 | ?2 = 2,0 | |
| Среднее | 1,0 | 0,999998 | 0,0 | 0,0 | 2,0012 | 10,001 | 3,0 | 2,0 |
| Стандартное отклонение | 0,0 | 4,47•10-6 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| Дисперсия выборки | 0,0 | 2•10-11 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| Минимум | 1,0 | 0,99999 | 0,0 | 0,0 | 2,0012 | 10,001 | 3,0 | 2,0 |
| Максимум | 1,0 | 1,0 | 0,0 | 0,0 | 2,0012 | 10,001 | 3,0 | 2,0 |
Таблицы тестовых данных были образованы N значениями функции в зависимости от d переменных (табл. 4). Аппроксимация производилась по ограниченной выборке из k табличных значений дробно-степенным рядом Пюизё
![]()
где управляемые параметры ? обозначены как ![]() причем
причем
для d=1, ![]() для d=2,
для d=2, 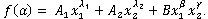
Аппроксимация табличных данных также выполнена методом Ньютона. Метод Ньютона - это бесконечношаговый алгоритм второго порядка, основанный на замене минимизируемой функции квадратичной частью ряда Тейлора [11], поэтому его использование для аппроксимации дробно-степенным рядом, если удается исключить нулевые значения аргументов, обеспечивает устойчивость вычислительного процесса.
Точность аппроксимации рассчитывалась по формуле ![]() , где
, где ![]() и
и ![]() – суммы расчетных и табличных значений критериев оптимальности.
– суммы расчетных и табличных значений критериев оптимальности.
Таблица 4.
Результаты аппроксимации табличных данных методом КГА и методом Ньютона.
| d | N | k | r | Фт | Метод КГА | Метод Ньютона | |||
| Фр | S | ?, % | Фр | ?,% | |||||
| 1 | 41 | 12 | 2 | 110,6 | 121,5 | 38 | -9,86 | 121,5 | -9,86 |
| 2 | 38 | 7 | 7 | 1,464 | 1,454 | 790 | -0,69 | 1,466 | 0,14 |
| 3 | 23 | 4 | 19 | 8,92 | 8,90 | 674 | -0,27 | 8,91 | -0,07 |
| 4 | 594 | 38 | 25 | 1094,6 | 1100,3 | 1004 | 0,51 | 1071,3 | -2,13 |
Анализ полученных результатов и выводы.
Предложенный метод аппроксимации использует компания «Weber Engineering» в практике проектирования технологических процессов, когда по ограниченному числу рассчитанных в САМ-системах или полученных хронометражом норм времени обработки деталей из листа необходимо достоверно определить время обработки всей программы деталей [12]. В табл. 4 представлены задачи, решенные в ряде проектов.
Первый тест (d=1) - определение периметра детали из листа по площади ее поверхности. Тестовая таблица содержала значения площади поверхности и периметра для 41 детали (N=41). Сумма всех периметров равнялась 110,6 мм. (Фт = 110,6). Использованием выборки из 12 деталей (k = 12) методом аппроксимации получена величина периметра всех деталей, равная 121,5 мм. (Фр=121,5). Погрешность аппроксимации не превысила 10%.
Второй тест (d=2) – определение времени обработки деталей (мин) на координатно-револьверном прессе в зависимости от количества ударов инструмента (x1) и количества смен инструмента (x2), необходимых для изготовления детали. Аппроксимация с использованием выборки из 7 деталей позволила рассчитать общее время обработки 38 деталей с погрешностью, менее 1%.
Третий тест (d=3) – определение времени гибки деталей (мин) на прессе для свободной гибки в зависимости от максимальной высоты полки (x1), массы детали (x2) и количества линий гибки (x3). Аппроксимация с использованием выборки из 4 деталей позволила рассчитать общее время обработки 23 деталей с погрешностью, менее 0,5%.
Четвертый тест (d=4) – время резки детали (мин) на машине для лазерной резки в зависимости от толщины листа (x1), периметра внутренних и наружных контуров (x2), предела прочности материала листа при растяжении (x3) и количества врезок (x4). Аппроксимация с использованием выборки из 38 деталей позволила рассчитать общее время обработки 594 деталей с погрешностью, около 0,5%.
Результаты тестирования показывают, что использование КГА для аппроксимации времени обработки на различном оборудовании дробно-степенными рядами позволяет выполнить расчеты с погрешностью, допустимой для практического использования. Это значительно сокращает время проектирования.
Использование метода Ньютона, также обеспечивает высокую точность аппроксимации, причем время вычислений у этого метода гораздо меньше. Для сравнения: решение тестовых задач методом КГА для d=1 составило 0,48 мин; для d=2 – 7,78 мин; для d=3 - 8,27 мин; для d=4 – 1 час 3 мин; время расчета методом Ньютона не превышало 0,5 мин. для всех тестовых задач. Это объясняется тем, что увеличение количества управляемых параметров модели (с r = 2 до r = 25, табл. 4) значительно увеличивает число циклов поиска (с S = 38 до S = 1004, табл. 4). Однако, решение задач аппроксимации метод Ньютона имеет недостаток – точность расчета зависит от выбора «начальной точки»: в процессе тестирования установлено, что в зависимости от значений управляемых параметров, с которых начинаются вычисления, в случае мультимодальной целевой функции (d > 1) погрешность аппроксимации составляла более 100%. Выполнить тесты с погрешностью, показанной в табл. 4 позволил длительный подбор начальных значений управляемых параметров. Работа алгоритма по методу КГА не требует задавать начальные значения управляемых параметров. Они устанавливаются в процессе пассивного поиска минимума и корректируются при сужении и расширении интервалов неопределенности.
Литература
- Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями качества. – М.: Наука, 1981. – 110 с.
- Статников И.Н., Фирсов Г.И. ПЛП-поиск - эвристический метод решения прикладных задач оптимизации // Практика применения научного обеспечения в образовании и научных исследованиях. - Санкт-Петербург: СПбГУ, 2003. - С. 54 - 57.
- Karaboga D. An idea based on honey bee swarm for numerical optimization. Technical report - TR06, Erciyes University, Engineering Faculty, Computer Engineering Department 2005.
- Pham D.T., Ghanbarzadeh A., Koc E, Otri S, Rahim S., Zaidi M. The Bees Algorithm. Technical Note, Manufacturing Engineering Centre, Cardiff University, UK, 2005
- Гришин А. А., Карпенко А. П. Исследование эффективности метода пчелиного роя в задаче глобальной оптимизации. Электронное научно-техническое издание «Наука и образование», 08 августа 2010.
- Ворожейкин А.Ю., Семенкин Е.С. Вероятностный генетичнский алгоритм для задач многокритериальной оптимизации. // Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева. 2007 №3, стр 41-45.
- Исаев С.А., Виндман П.А. Оптимизация многоэкстремальных одномерных функций с помощью генетических алгоритмов. Вестник Нижегородского университета им. Н.И. Лобачевского. Серия: Математическое моделирование и оптимальное управление. 2003 №1. С. 180 – 189.
- Курносова Е.Е., Полупанов А.А. Методы повышения качества решений в эволюционно-генетических алгоритмах. Известия Южного федерального университета. Технические науки. 2009. Т. 93. 34. С. 62-66.
- Дмитриев С.В. Об эффективном взаимодействии генетического алгоритма и метода Хука-Дживса для решения многомерных задач оптимизации. ISSN 1813-7903. Вестник ИжГТУ. 2007. №1. С. 58-63.
- Тенеев В.А. Решение задачи многокритериальной оптимизации генетическими алгоритмами. ISSN 1813-7911. Интеллектуальные системы в производстве. 2006. №2. С. 103-109.
- Тлибеков А.Х., Досько С.И. Прикладные задачи моделирования и оптимизации механических систем. Учебное пособие для аспирантов и магистров. ISBN 978-3-8473-9944-5. Palmarium Academic Publishing, 2012. - 252 с.
- Тлибеков А.Х. Эффективность проекта модернизации производства деталей из листа // Металлообработка. 2012. №3 (69), с. 45-51.